Degrees of Freedom Pearsons s R Dichotomous and Continuous N
Problem Statement
Perhaps you would like to test whether there is a statistically significant linear relationship between two continuous variables, weight and height (and by extension, infer whether the association is significant in the population). You can use a bivariate Pearson Correlation to test whether there is a statistically significant linear relationship between height and weight, and to determine the strength and direction of the association.
Before the Test
In the sample data, we will use two variables: "Height" and "Weight." The variable "Height" is a continuous measure of height in inches and exhibits a range of values from 55.00 to 84.41 (Analyze > Descriptive Statistics > Descriptives). The variable "Weight" is a continuous measure of weight in pounds and exhibits a range of values from 101.71 to 350.07.
Before we look at the Pearson correlations, we should look at the scatterplots of our variables to get an idea of what to expect. In particular, we need to determine if it's reasonable to assume that our variables have linear relationships. Click Graphs > Legacy Dialogs > Scatter/Dot. In the Scatter/Dot window, click Simple Scatter, then click Define. Move variable Height to the X Axis box, and move variable Weight to the Y Axis box. When finished, click OK.

To add a linear fit like the one depicted, double-click on the plot in the Output Viewer to open the Chart Editor. Click Elements > Fit Line at Total. In the Properties window, make sure the Fit Method is set to Linear, then click Apply. (Notice that adding the linear regression trend line will also add the R-squared value in the margin of the plot. If we take the square root of this number, it should match the value of the Pearson correlation we obtain.)
From the scatterplot, we can see that as height increases, weight also tends to increase. There does appear to be some linear relationship.
Running the Test
To run the bivariate Pearson Correlation, clickAnalyze > Correlate > Bivariate. Select the variables Height and Weight and move them to the Variables box. In the Correlation Coefficients area, select Pearson. In the Test of Significance area, select your desired significance test, two-tailed or one-tailed. We will select a two-tailed significance test in this example. Check the box next to Flag significant correlations.
Click OK to run the bivariate Pearson Correlation. Output for the analysis will display in the Output Viewer.
Syntax
CORRELATIONS /VARIABLES=Weight Height /PRINT=TWOTAIL NOSIG /MISSING=PAIRWISE. Output
Tables
The results will display the correlations in a table, labeled Correlations.
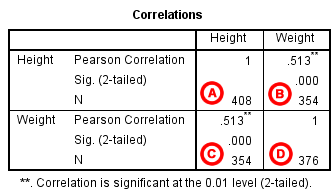
A Correlation of Height with itself (r=1), and the number of nonmissing observations for height (n=408).
B Correlation of height and weight (r=0.513), based on n=354 observations with pairwise nonmissing values.
C Correlation of height and weight (r=0.513), based on n=354 observations with pairwise nonmissing values.
D Correlation of weight with itself (r=1), and the number of nonmissing observations for weight (n=376).
The important cells we want to look at are either B or C. (Cells B and C are identical, because they include information about the same pair of variables.) Cells B and C contain the correlation coefficient for the correlation between height and weight, its p-value, and the number of complete pairwise observations that the calculation was based on.
The correlations in the main diagonal (cells A and D) are all equal to 1. This is because a variable is always perfectly correlated with itself. Notice, however, that the sample sizes are different in cell A (n=408) versus cell D (n=376). This is because of missing data -- there are more missing observations for variable Weight than there are for variable Height.
If you have opted to flag significant correlations, SPSS will mark a 0.05 significance level with one asterisk (*) and a 0.01 significance level with two asterisks (0.01). In cell B (repeated in cell C), we can see that the Pearson correlation coefficient for height and weight is .513, which is significant (p < .001 for a two-tailed test), based on 354 complete observations (i.e., cases with nonmissing values for both height and weight).
Decision and Conclusions
Based on the results, we can state the following:
- Weight and height have a statistically significant linear relationship (r=.513, p < .001).
- The direction of the relationship is positive (i.e., height and weight are positively correlated), meaning that these variables tend to increase together (i.e., greater height is associated with greater weight).
- The magnitude, or strength, of the association is approximately moderate (.3 < | r | < .5).
Source: https://libguides.library.kent.edu/spss/pearsoncorr

0 Response to "Degrees of Freedom Pearsons s R Dichotomous and Continuous N"
Post a Comment